what type of element is used to gather light in large astronomical telescopes?

Physics 320

Astrophysics I:  Lecture #3

Prof. Dale E. Gary NJIT

Telescopes and Detectors

Lenses, Mirrors and Optics

Telescopes come in two basic types: refracting telescopes (using a lens as its principal element: i, ii, three ) and reflecting telescopes (using a mirror as its master element: 1, 2, iii). Simple ray tracing techniques exist for determining for a given optic (either a lens or a mirror) where an epitome forms, given an epitome altitude.  The method is illustrated in the diagrams below.

The relationship between focal distance f , object distance p , and image altitude q , is given by the formula:

1/f = i/p + 1/q

which can be verified every bit consequent with the above rules through unproblematic geometry (homework problem 6.ii). Another important formula is the lens-maker'southward formula :

1/f _l = (n _l - 1) (1/R _i + ane/R ₂ )

where n _l is the alphabetize of refraction at wavelength l, and R ₁ and R ₂ are the radii of curvature of the lens (negative radius for a diverging lens). Note that this formula assumes the lens is in a vacuum (works approximately for air). If the lens is in a medium with index of refraction n ₀ , and so the first term in parentheses on the right should be (n _l - north ₀)/north ₀. Note that the alphabetize of refraction depends on wavelength (meet http://refractiveindex.info/), so in general a lens will accept a different focal length for red light ( l ~ 750 nm) than for bluish low-cal ( l ~ 450 nm). This causes chromatic aberation , which can be combatted by using an achromatic doublet, or an apochromatic triplet lens. An important belongings of mirrors is that all wavelengths are reflected the aforementioned, so mirror-based telescopes do not suffer from chromatic aberation.

An important number for a telescope's main lens or mirror (called an objective ), is its f ratio, which is simply the ratio of the focal length to the diameter D of the objective

f ratio = f/D.

In the to a higher place diagrams, the f ratio is about 1, but for optical telescopes it is more typically about 10.  (For radio telescopes, information technology is normally less than ane, typically 0.four.  Why do you think that might be?)

The arrows in the above drawings represent an extended object, which covers some angular altitude in front end of the lens.  If this were the Moon, say, it would cover 1/ii degree in the sky.  When nosotros make an paradigm, information technology likewise covers some athwart altitude from the lens, and if nosotros place a detector at that place (say a piece of photographic film), the image will take some linear size.  Now, the Moon can be considered to be at infinity (that is, d _o is much larger than d _i ), so the image of the Moon will occur at the focal distance f (which is why it is called the focus).  In this case, the linear size per degree of athwart size of the image at the image airplane (called the plate scale ) is merely

south = 0.01745 f

where the constant 0.01745 is just the number of radians in a caste, and f is the focal length of the objective.  The linear size of an image will be due south a , where a is the angular size of the object in degrees.

Example:
Say we have a telescope of 8 inch discontinuity, and f ratio of 10 (also referred to as f / ten).  How large will the Moon's image appear on a piece of photographic film at the focus?

The focal distance f is 80 in, and so the image volition exist

s a = 0.01745 a f = 0.01745 (ane/2 degree) (80 in) = 0.seven in

Telescopes

You will frequently hear someone ask, "What power is that telescope?".  This is a relatively meaningless question, and indicates someone who does not understand the principles of optics.  Practice non be ane of these people!  Their confusion is understandable--low-end telescopes are often advertised by their "power,"  by which is meant their magnification gene.  You volition never see a truthful astronomical telescope advertised this mode.  What is actually important is the light-gathering power of a telescope, not its magnification.  The light-gathering power is important, because this is what limits how faint an object i can see.  The larger the area of the objective, p D ² /four, the larger the corporeality of light gathered.  The light-gathering power is not a fixed number, but is expressed in comparing with another optical system, say your eye.  Your pupil has a maximum size of near 0.5 cm, and then the light-gathering ability of an 8" telescope (diameter 20.3 cm) is

LGP = (20.3/0.5) ^two = 1650.

The principal part of the telescope is to take all of this light and concentrate it into your center (or an equivalent camera). In this case, a telescope would gather 1650 times as much light as your naked eye. A 2d of import measure of a telescope also scales with its discontinuity--the resolving ability .  This depends on the wavelength of light that we are trying to prototype, and is given in angular units, arcseconds, past

RP = 1.22 (206265 l/D) arcsec

where the abiding 206265 is the conversion factor from radians to arcseconds.  The factor of i.22 is due to the fact that the aperture is circular.  For a rectangular aperture the factor would be i.0, but grinding rectangular lenses is non easy!

Example
What is the resolving power of our 8" telescope in the optical ( l ~ 500 nm)? viii" is twenty.3 cm, or 0.203 thou, so the resolving power would exist:

RP = 1.22 (206265 l/D) = 1.22 (206265)(5x10 ^-7 m/0.203 m) = 0.62"

Annotation, yet, that the atmosphere usually limits the resolution to nigh 1", and so having a telescope much larger than 8" does non assistance in resolution unless we either are in a higher place the temper or tin correct for the atmosphere.  A larger telescope does, notwithstanding, help in light-gathering power.

What almost magnification?  As it turns out, any telescope can be any magnification power!  It does not depend at all on the discontinuity, or size, of the telescope.  The magnification only depends on the ratio of the focal length of the objective f and the focal length of the eyepiece f _e :

MP = f / f _e .

Common eyepieces for telescopes are 26 mm and 12.five mm.  An f/x telescope of 8" aperture (203 mm) would provide corresponding magnifications of 78X and 162X for these two eyepieces.  Nonetheless, you lot could become the aforementioned magnifications with a 2" telescope simply past using eyepieces of 6.five mm and 3.ane mm focal length.  This is why request what "ability" a telescope has is not too meaningful.  Any telescope can have whatsoever power, depending on the eyepiece you cull.

Notwithstanding, there is an important relationship betwixt calorie-free-gathering power and magnification, which makes higher magnifications useless for small telescopes.  Think of the objective as gathering light, and the eyepiece as spreading it out again.  Although you can spread the light out indefinitely with smaller focal length eyepieces, this reduces the effulgence of the prototype until you reach a point where y'all cannot see it any longer.  This happens sooner, of course, for a smaller telescope, which gathers less light in the kickoff place.  If you desire to observe a faint, extended nebula, smaller powers are best (yous see more of the heaven at once, and the nebula is brighter).  If y'all want to find a brighter object, similar the Moon or a planet, yous can frequently get away with higher power.  However, at that place is no point magnifying the image beyond the resolution of the telescope (or the atmosphere), since you will merely magnify the distortions.

Detectors and Image Processing

Three types of detectors have historically been used in optical astronomy:

• Photographic Moving-picture show
• Photomultiplier Tubes
• Charge-Coupled Devices (CCDs)

The final blazon, the CCD, has for about applications replaced the other two (fifty-fifty in ordinary photography, with the rapid advances in digital cameras).  Ane reason is " quantum efficiency " or QE.  This expresses the ability of the detector to respond to photons, or light-quanta.  The human eye has a QE of about one%, significant that for every 100 photons that fall on our retina, but 1 is detected.  Photographic film has a similar QE, almost 1%.  Photomultipliers accept an efficiency betwixt x and 20%.  In contrast, CCDs accept much higher efficiencies, close to 100% in the red region of the spectrum.

Another reason for the increasing importance of CCDs is the large form-factors now available--upwardly to 10 million pixels (e.g. KAI-11002 chip, 4008 ten 2672).  It is common in astronomical detectors to identify multiple CCD chips side by side for extremely large format images (e.one thousand. the SDSS camera, LSST camera).

CCDs have other advantages too.  They are linear devices, and so that they give a precise measure of the number of photons falling on each pixel, over a very large range in brightness.  Ultimately, however, the pixels (quantum wells) will fill up, and the device saturates.  The electrons then spill over into neighboring pixels.  The image below shows an case of such saturation.

Two Sun-grazing comets plunge to their fiery decease
into the Sun.  The image of one of the comets has
saturated the CCD camera, and its calorie-free spills into
neighboring pixels, making a horizontal line antiquity.

CCDs also take the advantage of being purely digital, so they can exist controlled easily with computers, and their information can be manipulated digitally.

Signal to Racket

Photons obey Poisson statistics, meaning that the inflow of photons into a given pixel is a random process, just always positive (there are no negative photons).  The statistical fluctuations in the mean number of photons <N> have a standard divergence given by southward = <Northward> ^1/ii .  Thus, the signal to racket ratio is

South/N =  <North>/due south = <Due north> ^1/2 .

At present, the mean number of photons detected by a CCD pixel volition depend on the photon flux f _p (photons per second) x the integration time D t ten the breakthrough efficiency, so the signal to noise becomes:

South/N = (QE f _p D t) ^ane/2 .

For a given quantum efficiency, nosotros can increase the signal to noise by increasing the integration time.  Withal, to double the S/Northward, we must increase the integration time by a factor of 4.

An Example--The NJIT Observatory

The NJIT observatory has a reckoner-controlled 10" Meade LX200-GPS telescope.  We can utilise this telescope with an SBIG STL-1301 CCD camera for "deep-heaven" imaging, or utilise a simple webcam for planetary and lunar imaging.  The telescope is an f/10 system, and the two CCD cameras take the following specifications:

Some CCD Photographic camera Specifications

CCD	Kodak KAF-1301E	TouCAM Two VGA CCD
Pixel Array	1280 x 1024 pixels 20.4 x 16.4 mm	640 x 480 pixels iii.58 10 2.69 mm
Total Pixels	1,310,720	307,200
Pixel Size	16 x sixteen microns	5.6 x 5.6 microns
Full Well Capacity (NABG)	~120,000 east-	?
Dark Current	0.5e¯/pixel/sec at -xxx° C	?

What is the image scale of the KAF-1301E CCD (arcsec/pixel)?

The focal length is f = (f ratio)D = 10*ten in = 100 in. <= note these are inches!
The plate scale is due south = 0.01745 f = 1.75 inches/caste.
One pixel is 16 microns, so this corresponds to an image scale of

(16 ten ten ^-six g/pixel)(3600"/caste)/[(ane.75 in)(ii.54 ten 10 ^-2 k/in)] = one.29"/pixel

What is the field of view of the CCD camera, in arcminutes?

The chip has 1280 x 1024 pixels, and each is 1.29", so this becomes 1659" x 1321", or in arcminutes: 27.6' x 22.0'.

Will the Galilean moons of Jupiter fit into the field of view when Jupiter is at opposition?

At opposition, Jupiter is four.2 AU from Globe, and is 71,400 km in radius.  This corresponds to an angular size, in arcsec, of 206265 (R/d) = 23".  The outer-most Galilean moon is Callisto, at 26.vi Jupiter radii, or 618".   This is smaller than the CCD field of view, so Jupiter and its moons will fit comfortably in the field of view. The planet would cover about 36 pixels of the paradigm.

A sampling of images taken past students with this organisation can be found here. Note that there is a whole host of other bug involved with taking good images, involving groundwork heaven brightness, flat-fielding, and bounty for image move.

We use the webcam for taking images (and movies) of the Moon and planets, because information technology has a far smaller plate scale (i.e. produces more magnified images). If the weather cooperates, nosotros will have an imaging session this week.

Spectroscopy

Spectrographs are used to split the light from an object into its dissever wavelengths, or colors.  Ane can determine the temperature of an object, for example, from the shape of its blackbody spectrum.  In addition, many objects emit spectral lines (narrow regions of the spectrum that are brighter than the background--emission lines; or darker--assimilation lines).  By identifying these lines we can decide what the object is made of, and by measuring them nosotros can determine the temperature, density, and speed (through the doppler effect) of the objects.  The spectrograph is an important tool of Astronomy.

The nearly mutual type of spectrograph is the grating spectrograph, which uses a diffraction grating (basically a set up of extremely closely-spaced ruled lines).  Diffraction at the edges of each space between the lines causes the light to be split into its component colors, and interference of the light from each set causes the spectrum to be divide into "orders".  For a simple grating, college orders are fainter, but the light into a item gild can be increased past "blazing" the grating (kind of a saw-tooth profile) at the appropriate angle.

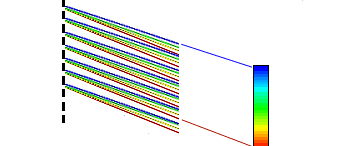
Diffraction into a loftier club.  In the direction shown by the bluish lines,
the blue light interferes constructively considering the beams all arrive at
the distant screen later having traveled distances different past an integral
number of wavelengths.  In the direction shown by the red lines, blue
light will go far later on traveling not-integer multiples of the wavelength,
and so the calorie-free interferes and the intensity drops to near zero.  Still, red
light arrives after traveling distances unlike by an integral number of
cherry-red wavelengths, then the ruby-red intensity is loftier in that direction.

As shown above, the direction for constructive interference into order m is given by

sin q = thousand 50/d ,

where d is the spacing between ruled lines on the grating.

What We Take Learned

The important formulas and quantities for telescopes are:

• Image formula 1/f = ane/d _o + 1/d _i
• Lens maker'due south formula one/f ₅₀ = (due north _l - ane) (1/R _i + 1/R ₂ )
• f Ratio f ratio = f/D
• Plate scale south = 0.01745 f
• Light gathering power LGP = (D/d _center ) ^two
• Resolving ability RP = ane.22 l/D (radians)
• Magnification factor MP = f / f _e

Another important formula is Signal to Dissonance ratio for CCDs:

• S/N = (QE f _p D t) ^one/2 .

westacottthaskilly.blogspot.com

Source: https://web.njit.edu/~gary/320/Lecture3.html

Share this post